Broglie Atomic Model Egenskaper och begränsningar

den Broglie atommodell föreslogs av den franska fysikern Louis Broglie 1924. I sin doktorsavhandling, sade han Broglie våg-partikeldualitet av elektroner, lägger grunden för våg mekanik. Broglie publicerade viktiga teoretiska fynd om materiens vågkroppsliga natur vid atomskala.

De Broglie senare uttalanden experimentellt demonstreras av forskare Clinton Davisson och Lester Germer 1927. Den våg teorin om elektron de Broglie bygger på Einsteins förslag på vågen egenskaper ljus med korta våglängder.

Broglie tillkännagav möjligheten att materia hade ett beteende som liknar ljusets ljus och föreslog liknande egenskaper i subatomära partiklar som elektroner.

Elektriska laddningar och banor begränsar amplituden, längden och frekvensen hos den våg som beskrivs av elektroner. Broglie förklarade rörelsen av elektroner runt atomkärnan.

index

• 1 Egenskaper hos Broglie-atommodellen
• 2 Davisson och Germer experiment
• 3 begränsningar
• 4 artiklar av intresse
• 5 referenser

Egenskaper hos Broglie-atommodellen

För att utveckla sitt förslag började Broglie från principen att elektroner hade en dubbel karaktär mellan våg och partikel, liknar ljus.

I detta avseende gjorde Broglie en jämförelse mellan båda fenomenen och baserade på de ekvationer som Einstein utvecklade för att studera ljusets vågform, angav han följande:

- Den totala energin hos foton och följaktligen den totala energin hos elektronen härrör från produkten av vågens frekvens och Plank-konstanten (6.62606957 (29) × 10 ^-34 Jules x sekunder), som detaljerad i följande uttryck:

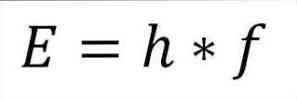
I detta uttryck:

E = elektronenergi.

h = Plank konstant.

f = frekvens av våg.

- Fotons linjära moment och därmed elektronen är omvänd proportionell mot våglängden, och båda storlekarna är relaterade genom Plank-konstanten:

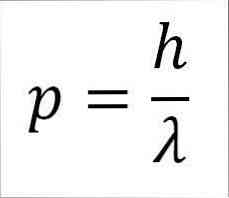
I detta uttryck:

p = linjärt moment av elektronen.

h = Plank konstant.

A = våglängd.

- Den linjära momentumet är produkten av partikelmassan med den hastighet som partikeln har vid dess förskjutning.

Om det föregående matematiska uttrycket omstruktureras som en funktion av våglängd har vi följande:

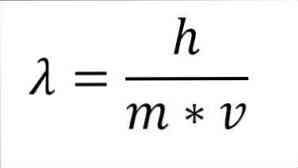
I nämnda uttryck:

A = våglängd.

h = Plank konstant.

m = elektronens massa.

v = elektronhastighet.

Eftersom h, Plankkonstanten, har ett litet värde, är våglängden A också. Följaktligen är det möjligt att ange att elektronens vågegenskaper endast uppträder vid atom- och subatomiska nivåer.

- Broglie bygger också på postulaten av Bohrs atommodell. Enligt sistnämnda är elektronernas banor begränsade och kan endast vara multiplar av heltal. sålunda:

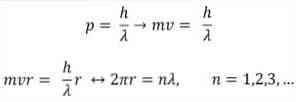
där:

A = våglängd.

h = Plank konstant.

m = elektronens massa.

v = elektronhastighet.

r = banans radie.

n = heltal.

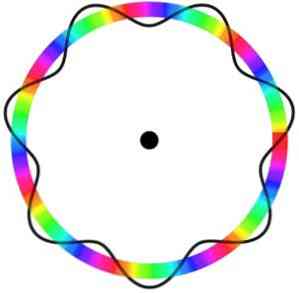
Enligt Bohr-modellen, som Broglie antas som en grund, om elektronerna beter sig som stående vågor, de enda tillåtna banor är de vars radie är lika med en heltalsmultipel av våglängden λ.

Därför uppfyller inte alla banor parametrarna som krävs för att en elektron ska kunna röra sig genom dem. Det är därför elektronerna kan bara resa i specifika banor.

Vågteorin för Broglie-elektronerna motiverade framgången med Bohrs atommodell för att förklara beteendet hos väteatomens enkla elektron.

Analogt belyser det också varför denna modell inte passade mer komplexa system, det vill säga atomer med mer än en elektron.

Davisson och Germer experiment

Den experimentella verifieringen av Broglie-atommodellen ägde rum 3 år efter det att den publicerades, 1927.

De framstående amerikanska fysikerna Clinton J. Davisson och Lester Germer bekräftade experimentellt teorin om vågmekanik.

Davisson och Germer utförde scatteringstester av en elektronstråle genom en nickelkristall och observerade diffraktionsfenomenet genom metallmediet.

Experimentet utfördes bestod av att utföra följande procedur:

- I första hand placerades ett aggregat med elektronstråle som hade en känd initial energi.

- En spänningskälla installerades för att påskynda rörelsen av elektroner, vilket ledde till en potentiell skillnad.

- Elektronstrålens flöde riktades mot en metallkristall; i detta fall nickel.

- Antalet elektroner som påverkade nickelkristallen mättes.

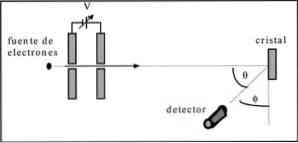
Vid slutet av försöket upptäckte Davisson och Germer att elektronerna dispergerades i olika riktningar.

Genom att upprepa experimentet med användning av metallkristaller med olika orienteringar upptäckte forskarna följande:

- Dispersionen av elektronstrålen genom metallkristallen var jämförbar med fenomenet interferens och diffraktion av ljusstrålarna.

- Reflektionen av elektronerna på slagkristallen beskrev den bana som teoretiskt skulle beskriva enligt teorin om elektronvågor i Broglie.

I syntesen visade experimentet av Davisson och Germer experimentellt den elektroniska dubbelvågpartikelnaturen.

begränsningar

Broglie-atommodellen förutsäger inte den exakta platsen för elektronen på banan i vilken den rör sig.

I denna modell uppfattas elektroner som vågor som rör sig runt omloppet utan en viss plats, som introducerar begreppet elektroniskt orbital.

Dessutom anser Broglie-atommodellen, som är analog med Schrödinger-modellen, inte om rotation av elektroner på sin axel (spinn).

Genom att ignorera elektronens inneboende vinkelmoment, försummas de rumsliga variationerna av dessa subatomiska partiklar..

I samma ordning med idéer tar inte denna modell hänsyn till förändringar i snabba elektroners beteende som en följd av relativistiska effekter.

Artiklar av intresse

Atommodell av Schrödinger.

Atommodell av Chadwick.

Atommodell av Heisenberg.

Atommodell av Perrin.

Atommodell av Thomson.

Atommodell av Dalton.

Atommodell av Dirac Jordanien.

Atommodell av Democritus.

Atommodell av Bohr.

referenser

1. Bohrs Quantum Theory och De Broglie Waves (s.f.). Hämtad från: ne.phys.kyushu-u.ac.j
2. Louis de Broglie - Biografisk (1929). © Nobelstiftelsen. Hämtad från: nobelprize.org
3. Louis-Victor de Broglie (s.f.). Hämtad från: chemed.chem.purdue.edu
4. Lovett, B. (1998). Louis de Broglie. Encyclopædia Britannica, Inc. Hämtad från: britannica.com
5. Atommodell av De Broglie. National University of Distance Education. Spanien. Hämtad från: ocw.innova.uned.es
6. Vågor av materia av Louis De Broglie (s.f.). Hämtad från: hiru.eus
7. Von Pamel, O. och Marchisio, S. (s.f.). Kvantmekanik National University of Rosario. Hämtad från: fceia.unr.edu.ar