Angular Displacement Formulas och lösta övningar

den vinkelförskjutning Den genereras när ett objekt rör sig efter en bana eller väg som har formen av en cirkel. Det skiljer sig från förskjutningen; medan vinkelförskjutningen mäter vinkeln som räknas, mäter förflyttningen avståndet.

Att beräkna vinkelförskjutningen hos ett objekt som rör sig längs en omkrets kan användas på två sätt: om den initiala och slutliga vinkeln är känd, då vinkelförskjutningen är subtraktionen mellan slutvinkel och den initiala vinkeln.

Om längden på förskjutningen (längden på den omkretsbågen som reste) och omkretsens radie är känd, ges vinkelförskjutningen med θ = l / r.

index

• 1 Formler
• 2 övningar
  • 2.1 Första övningen
  • 2.2 Andra övningen
  • 2.3 Tredje övning
• 3 referenser

formler

För att få de ovan beskrivna formlerna kan du se följande bilder:

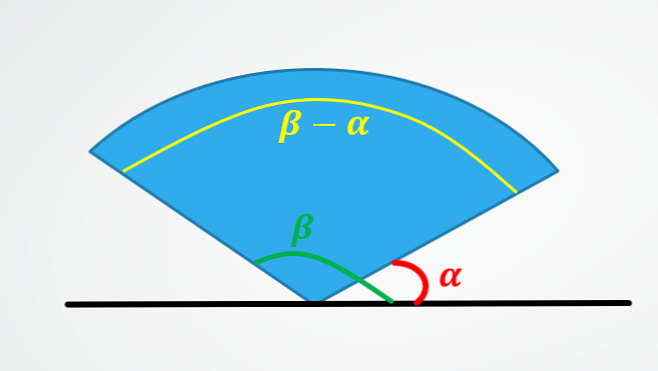
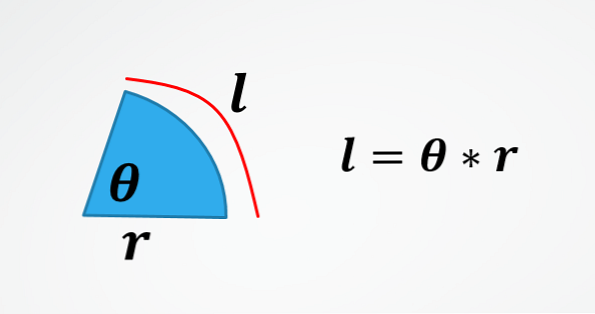
Den första visar varför vinkelförskjutningen är lika med subtraktionen av den slutliga vinkeln minus initialvinkeln.

I den andra bilden är formeln för längden på en cirkelbåg. Därför, genom att rensa θ får du den formel som beskrivs i början.

utbildning

Nedan följer några övningar där definitionen av vinkelförskjutning ska tillämpas och där de ovan beskrivna formlerna används.

Första träningen

Juan har kört ett avstånd på 35 meter på ett cirkulärt spår, vars radie är lika med 7 meter. Beräkna vinkelförskjutningen som Juan har gjort.

lösning

Eftersom avståndet på bågen reste och omkretsen av omkretsen är känd kan den andra formeln appliceras för att känna till vinkelförskjutningen gjord av Juan. Med hjälp av formeln som beskrivits ovan har du det θ = 35/7 = 5 radianer.

Andra övningen

Om du har det som Mario har åkt i sin bil hälften av ett cirkulärt tävlingsspår, vad är vinkelförskjutningen som Mario har gjort??

lösning

I denna övning kommer den första formeln att tillämpas. Eftersom det är känt att Mario har rest halvdelen av banan, kan det antas att han började loppet i 0 ° vinkeln och när han nådde mitt i cirkeln har han rest 180 °. Därför är svaret 180 ° -0 ° = 180 ° = π radianer.

Tredje övningen

María har en cirkulär pool. Din hund springer runt poolen som täcker ett avstånd på 18 meter. Om radie av poolen är 3 meter, vad är vinkelförskjutningen gjord av Marias maskot??

lösning

Eftersom poolen är cirkulär och du känner till radie av den, kan du fortsätta använda den andra formeln.

Det är känt att radien är lika med 3 meter, och avståndet som körs av husdjuret är lika med 18 meter. Därför utförs vinkelförskjutningen lika med θ = 18/3 = 6 radianer.

referenser

1. Basto, J.R. (2014). Matematik 3: Grundläggande analytisk geometri. Patria Editorial Group.
2. Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematik: ett problemlösande tillvägagångssätt för grundlärare. López Mateos Editores.
3. Bult, B., & Hobbs, D. (2001). Math lexikon (illustrerad utgåva). (F. P. Cadena, Trad.) Utgåvor AKAL.
4. Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometri. Reform av den övre cykeln hos E.G.B. Utbildningsdepartementet.
5. Schneider, W., & Sappert, D. (1990). Praktisk teknisk ritningsmanual: Introduktion till grunderna för industriell teknisk ritning. Reverte.
6. Thomas, G. B., & Weir, M. D. (2006). Beräkning: flera variabler. Pearson Education.